,The Mantel test (Mantel 1967; Mantel and Valand 1970) is an extremely versatile statistical test that has many uses, including spatial analysis. The Mantel test examines the relationship between two square matrices (often distance matrices) X and Y. The values within each matrix (Xij or Yij) represent a relationship between points i and j. The relationship represented by a matrix could be geographic distance, a data distance, an angle, a binary matrix, or almost any other conceivable data. Often one matrix is a binary matrix representing a hypothesis of relationships among the points or some other relationship (e.g., Xij may equal 1 if points i and j are from the same country and 0 if they are not). By definition, the diagonals of both matrices are always filled with zeros.
The basic Mantel statistic is simply the sum of the products of the corresponding elements of the matrices
,
where 
is the double sum
over all i and all j
where i ≠ j.
Because Z is can take on any
value depending on the exact nature of X
and Y, one usually uses a normalized
Mantel coefficient, calculated as the correlation between the pair wise
elements of X and Y.
Like any product-moment coefficient, it ranges from –1 to 1.
While more or less interpretable as a correlation coefficient, the significance of the normalized Mantel coefficient cannot be found from standard statistical tests because the observations within the matrices are not independent. In general, the significance is tested through a randomization test by randomly permuting the order of the elements within one matrix (rows and columns are permuted in tandem). When the number of points is large (n > 40), it is possible to transform the Mantel statistic into a t statistic. The significance of t is obtained from an asymptotic approximation of the t-test, which is more reliable for larger n. See Fortin and Gurevitch (1993) and Dutilleul et al. (2000) for more information on the Mantel test.
The basic Mantel test allows for the comparison of two matrices. A number of extensions to include additional matrices have been developed (Dow and Cheverud 1985; Hubert 1987; Manly 1968, 1997; Smouse et al. 1986). One extension is to perform a partial Mantel test, where a third (or more) matrix is held constant while the relationship of the first two is determined (Smouse et al. 1986). This test is done by regressing the elements of X and Y onto the additional matrix (multiple regression for more than one additional matrix), and using the residuals from the regressions as the input for the standard Mantel test.
The traditional approach to estimating significance of a partial Mantel test is to permute the rows and columns of the residual matrices (e.g., this was the method used in PASSaGE 1). While computationally quick (relative to other approaches), this method has been found to have poor statistical properties (Legendre 2000). In this version of PASSaGE, one of the original matrices is permuted prior to the regression (or multiple regression), the regression for that matrix is repeated and then the partial Mantel correlation determined. While slower than the original approach, this should lead to more accurate estimates of the significance or partial Mantel statistics. See Oden and Sokal (1992) and Legendre (2000) for more information on partial Mantel tests.
The Mantel permutation tests are traditionally performed by comparing the magnitudes of Z, which is fine for one-tailed tests, but can give misleading results for two-tailed tests. For a two-tailed permutation test, it is important to transform each Z to an r, which may be more computationally intensive, particularly for partial Mantel tests (for simple pairwise tests it should make little difference).
| Menu: | Analysis→Basic→Mantel Test |
| Button: |  |
| Batch: | Mantel |
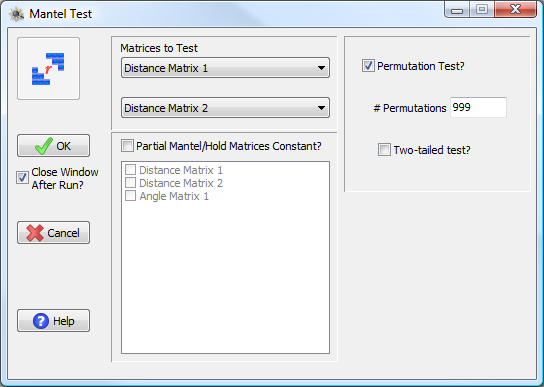
Mantel Test window.
The basic input for a Mantel test is a pair of square matrices: these can be distance matrices, angle matrices, or binary matrices. All matrices must be the same size. Optionally, additional matrices can be specified to hold constant. You may also choose to perform permutation tests (recommended) for the determination of significance. You have the option of one-tailed or two-tailed permutation tests (the two-tailed tests may take a lot longer). The output of a Mantel test includes both the observed Z and the Mantel correlation. It lists the results of the asymptotic t-test and significance.
Mantel Test
Matrix 1: Geo Distance Matrix
Matrix 2: Data Distance Matrix
Matrices are 355 x 355
Observed Z = 3894672599.85108
Correlation = 0.31206
t = 17.81190
Left-tailed p = 1.00000
Right-tailed p = 0.00000
Two-tailed p = 0.00000
Permutation Results (999 permutations)
# of Permutations < Observed = 999
# of Permutations > Observed = 0
# of Permutations = Observed = 1
Left-tailed p = 1.00000
Right-tailed p = 0.00100
Example of Mantel Test output.
If permutation tests were performed, results follow the asymptotic test. They include the number of times replicates (including the observed value) are less than, greater to, or equal to the observed value, and P-values for one-tailed tests (both left and right) and, if requested, for the two-tailed test.